Normal Distribution
Definition
기초 통계에서 빠질 수 없는 Normal distribution(정규 분포)에 대해 정리합니다.
독일 수학자 가우스(1777 ~ 1855)가 처음 개념을 정립해서 '가우시안 분포'라고 하기도 합니다.
우선 생긴건 이렇게 생겼습니다.

이 종모양의 확률밀도함수를 어떻게 해석하고 의미를 부여하느냐에 따라 상당히 많은 것을 할 수 있습니다.
자연 현상이나 사회 현상에서 나타나는 여러가지 통계자료를 히스토그램으로 그리면,
자료의 개수를 늘릴수록, 계급의 크기를 작게 할수록 좌우대칭인 종모양의 곡선에 가까워집니다.
데이터 분석이라고 하는 것이, 데이터의 특성을 파악하고 분포에 따른 분류 작업이 주를 이룹니다.
그래서 보통 데이터 분포가 Normal Distribution을 따르면 종모양의 중심에서 멀어지는 구간에 따라 특성을 달리 가져가도록 의사 결정할 수 있습니다.
이러한 결정을 자동화하고 모델을 만들면, 머신 러닝 모델이 됩니다.
Normal Distribution의 수식은 다음과 같습니다.
\(f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{\frac{-(x-m)^{2}}{2\sigma^{2}}}\) ( -∞ < x < ∞ )
Expression
\(N(m, \sigma^{2})\) = mean이 m 이고 sd가 σ 인 Normal Distribution
Parameters
x : X의 확률변수 ( -∞ < x < ∞ )
m : x의 mean
σ : x의 sd(standard deviation)
e : 2.718281
Characteristic
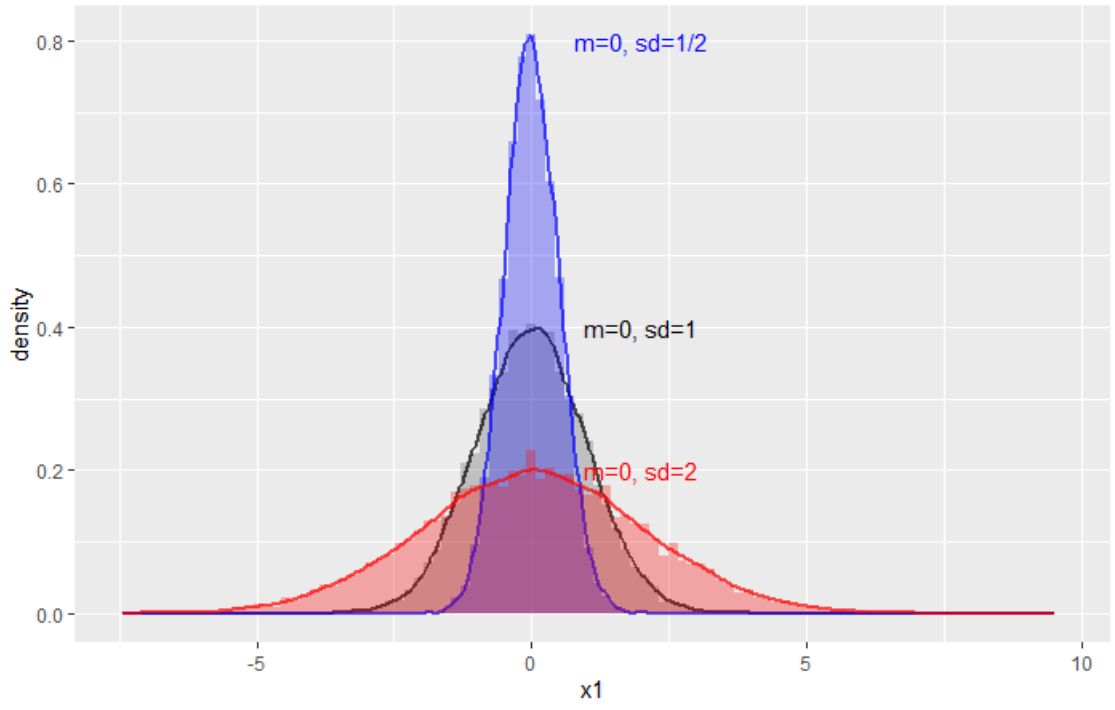
1. mean 일정, sd 가변
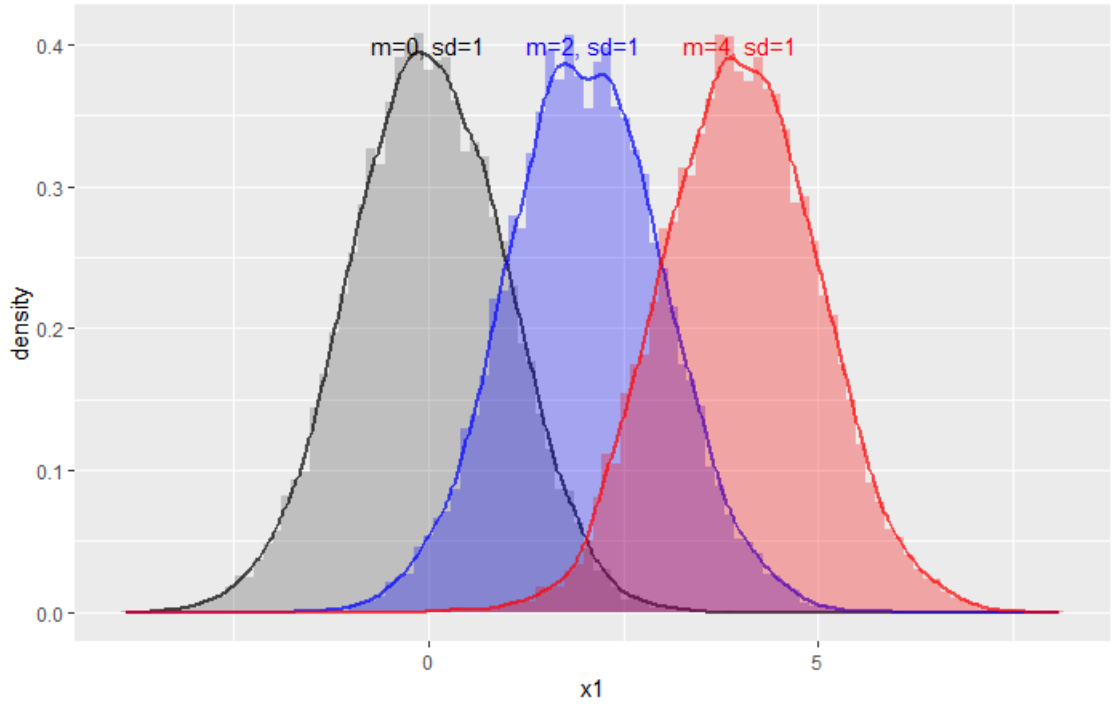
2. mean 가변, sd 일정
Standard Normal Distribution
Difinition
Normal Distribution \(N(m, \sigma^{2})\) 에서 m=0, σ=1일때 Standard Normal Distribution이라고 함
PDF 는 \(f(z)=\frac{1}{\sqrt{2\pi}}e^{\frac{-z^{2}}{2}}\) ( -∞ < z < ∞ )
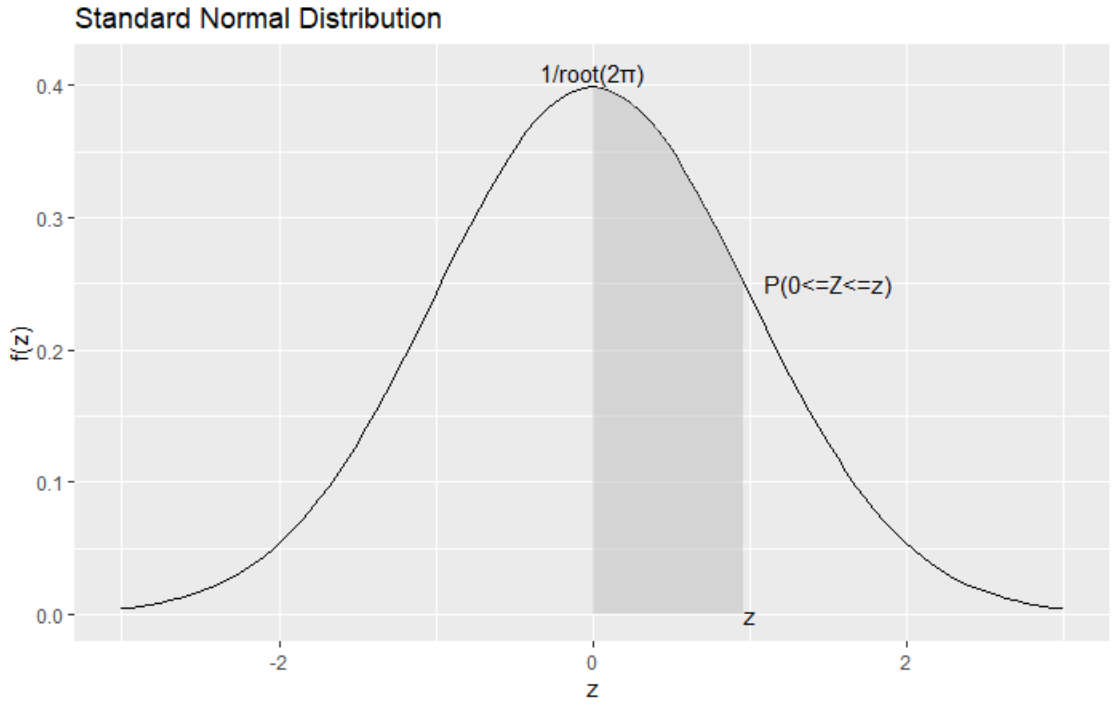
Characteristic
임의의 양수 z에 대해 연속확률변수 Z가 0이상 z이하의 값을 가질 확률 \(P(0\leq Z \leq z)\)는 위 graph에서 빗금 부분의 넓이
확률변수 X가 Normal Distribution \(N(m, \sigma^{2})\)을 따를 때, 확률변수 Z는 Standard Normal Distribution N(0, 1) 을 따름
\(Z=\frac{X-m}{\sigma }\)
'머신러닝 > 통계' 카테고리의 다른 글
| 통계 - T test (0) | 2021.03.26 |
|---|---|
| 통계 - Expectation E(X) (0) | 2021.03.24 |
| 통계 - Likelihood (0) | 2021.03.24 |
| 통계 - Statistical Estimation (0) | 2021.03.20 |
| 통계 - Random Variable, Probability Distribution, PDF, CDF, PMF, CMF (0) | 2021.03.13 |