모집단(Population)에서 표본(Sample)을 Random Sampling으로 추출하고, 추출된 표본에 대한 신뢰도에 대한 개념을 정리합니다.

Sample(표본)
Definition
Sample(표본) = 모집단의 부분집합
모집단에서 크기가 n인 표본 \(X_{1}, X_{2}, ... X_{n}\) 을 임의추출 하였을 때,
표본평균 \(\overline{X}=\frac{1}{n}\sum_{i=1}^{n}X_{i}\)
표본분산 \(S^{2}=\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\overline{X})^2\)
표본표준편차 \(S=\sqrt{S^{2}}\)
Sample Mean(표본 평균)의 평균, 분산, 표준 편차, 표준 오차
Definition
모평균이 m, 모분산이 \(\sigma^{2}\)인 모집단에서 크기가 n인 표본을 복원 추출할 때, 표본평균\(\overline{X}\)에 대해,
\(E(\overline{X})=m\)
\((V(\overline{X})=E((\overline{X}-\mu)^2)=\frac{\sigma^{2}}{n}\)
\(\sigma(\overline{X})=\sqrt{E((\overline{X}-\mu)^2)}=\frac{\sigma}{\sqrt{n}}\)
모분산=\(\sigma^{2}\)
※ 표준 오차(SE - Standard Error) : 표본 평균의 표준 편차.
- 표본평균은 모평균에 대한 추정값, 모평균은 참값
- 변량이 표본평균일 때, (변량-평균) = (추정값-참값)을 의미 (추정값-참값)은 오차
표준 편차 vs 표준 오차
※ 표준 편차 : (변량-평균)의 제곱의 평균에 루트
※ 표준 오차 : (추정값-참값)의 제곱의 평균에 루트
\(s(\overline{X})=\frac{s}{\sqrt{n}}\)
모분산의 추정치=\(s^{2}\)
※ 표본 평균의 표준 오차"(SEM - Standard Error of Mean) : 표본 평균 분포의 표준 편차
Charateristic
모집단의 분포가 정규분포를 따르면 표본평균 \(\overline{X}\)는 정규분포 \(N(m,\frac{\sigma^2}{n})\)를 따름
모집단의 분포가 정규분포를 따르지 않더라도, 표본의 크기 n이 충분히 크면(n이 30이상) 표본평균 \(\overline{X}\)는 근사적으로 정규분포 \(N(m,\frac{\sigma^2}{n})\)를 따름
Statistical Estimation(통계적 추정)
Definition
표본에서 얻은 정보를 이용하여 모집단의 특성을 확률적으로 추측하는 것
정규분포 \(N(m,\sigma^2)\)을 따르는 모집단에서 임의추출한 크기가 n인 표본으로부터 얻은 표본평균이 \(\overline{X}\)일 때, 모평균 m의 신뢰구간
신뢰도 95%의 신뢰구간: \(\overline{X}-1.96\frac{\sigma}{\sqrt{n}}\leq m \leq \overline{X}+1.96\frac{\sigma}{\sqrt{n}}\)
신뢰도 99%의 신뢰구간: \(\overline{X}-2.58\frac{\sigma}{\sqrt{n}}\leq m \leq \overline{X}+2.58\frac{\sigma}{\sqrt{n}}\)
※ 실제로 모집단의 표준편차 σ를 모르는 경우가 대부분, 표본표준편차S 를 이용해도 신뢰도는 성립.
Charateristic
Confidence Interval(신뢰구간)은 넓게 잡으면 더욱 신뢰할 수 있는 추정이라고 할 수 있으나, 추정으로서의 가치는 떨어짐
막연한 추정은 의미가 없고, 어느 정도의 오차를 허용하더라도 적당한 크기의 구간으로 평균을 추정하는 합리적인 방법이 필요
Inducement
정규분포 \(N(m,\sigma^{2})\) 을 따르는 모집단에서 크기가 n인 표본을 임의추출하였을 때, 표본평균 \(\overline{X}\) 는 정규분포 \(N(m,\frac{\sigma^{2}}{n})\)을 따름
확률변수 \(\overline{X}\) 를 표준화한 확률변수 \(Z=\frac{\overline{X}-m}{\frac{\sigma}{\sqrt{n}}}\) 은 표준정규분포 N(0, 1)을 따름
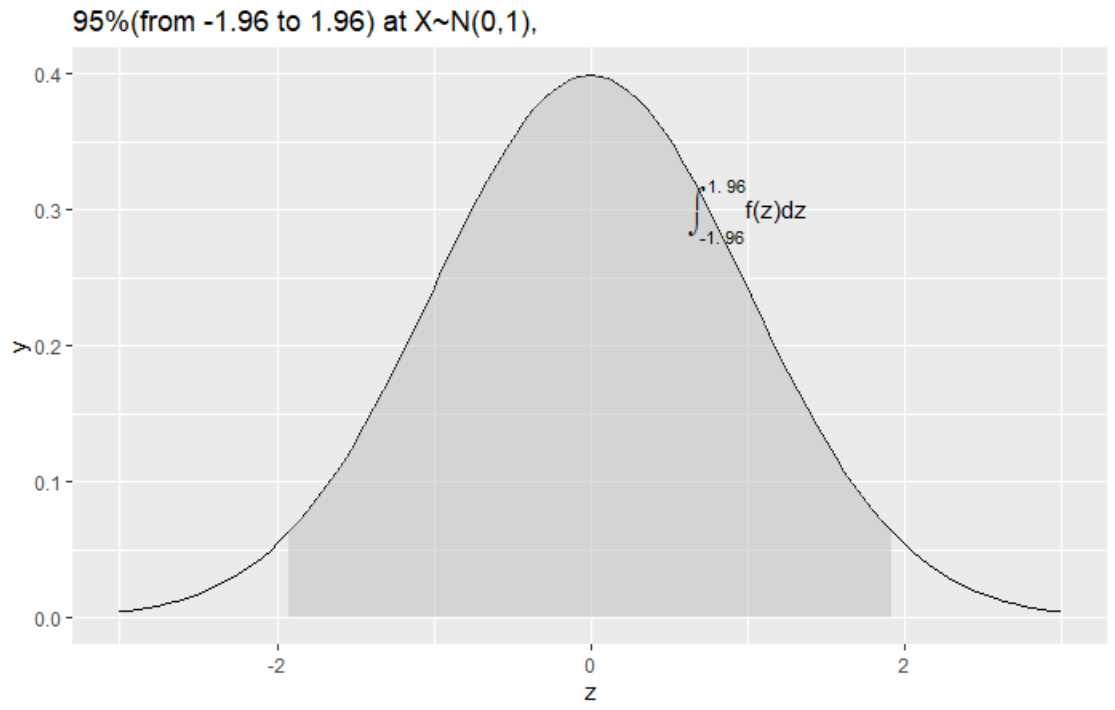
\(P(-1.96\leq\frac{\overline{X}-m}{\frac{\sigma}{\sqrt{n}}}\leq 1.96)=0.95\)
\(P(\overline{X}-1.96\frac{\sigma}{\sqrt{n}}\leq m \leq \overline{X}+1.96\frac{\sigma}{\sqrt{n}})=0.95\)
Sample Size Calculator
위의 추정 지식을 바탕으로, 이제는 모집단의 전체 수 N을 알 때, 원하는 신뢰도와 신뢰구간의 필요한 sample 개수를 알아낼 수 있다.
표본 sample 개수가 필요한 경우는 선거 조사 시 모든 국민을 대상으로 조사할 수 없으므로 필요한 표본을 고르는 예가 있을 수 있음.
Machine Learning 에서는 전체 데이터의 분포를 알고 싶은데, computing power 또는 시간 절약의 이유로 적절히 random sampling 하여 대략의 분포를 알고자 할 때 쓰임.
Formula
공식은 다음과 같은데 유도 과정 등에 대해서는 아직 100% 이해는 하지 못하였다. 관련 parameter들에 관한 정보는 아래를 참조하자.

z : z score (ex : 1.96)
p : observed percentage - 관찰치(응답 비율)로 보통 최대 표본오차를 구하기 위해 0.5를 사용 (ex : 0.5)
N : population size (ex : 100000)
e : margin of error (ex : 0.02)
오차 한계 = \(z\times \frac{\sigma}{\sqrt{n}}\)
표본 오차 정의
표본오차 = ±(Z)*SQRT(표본분산/표본수)
표본분산 = (응답 비율)*(1–응답 비율)
Z = 1.96: 신뢰수준 95%, 2.58: 신뢰수준 99%
SQRT: square root, 제곱근
예를 들어, 표본수 2,000명에서 예상 응답 비율 50%라면 표본오차는 ±2.19%포인트로 계산됩니다.
±2.19 = ±(1.96)*SQRT[(0.5)*(1-0.5)/2000]
※ 아래 사이트 참조했습니다.
www.gallup.co.kr/gallupdb/faqContents.asp?seqNo=107
www.nownsurvey.com/calculator/
Reference
아래는 해당 공식으로 원하는 Confidence Level 및 Confidence Interval 에서의 sample size를 쉽게 구할 수 있는 기능을 제공하는 사이트
www.surveysystem.com/sscalc.htm
www.calculator.net/sample-size-calculator.html?type=1&cl=95&ci=5&pp=50&ps=13370&x=60&y=4%EF%BB%BF
ko.wikipedia.org/wiki/%ED%91%9C%EC%A4%80_%EC%98%A4%EC%B0%A8
'머신러닝 > 통계' 카테고리의 다른 글
| 통계 - T test (0) | 2021.03.26 |
|---|---|
| 통계 - Expectation E(X) (0) | 2021.03.24 |
| 통계 - Likelihood (0) | 2021.03.24 |
| 통계 - Random Variable, Probability Distribution, PDF, CDF, PMF, CMF (0) | 2021.03.13 |
| 통계 - Normal distribution 어렵지 않아요 (0) | 2021.03.07 |