확률 변수, 확률 분포, PDF, CDF 는 통계에서 항상 따라 다니지만, 개념이 제대로 안집히면 항상 햇갈리고 고생하는 용어이며 개념입니다.
이번 기회에 용어 및 개념 정리를 합니다.
※ 통계는 개념 못지 않게 Definition이 중요한 것 같습니다. 햇갈리지 않게 용어에 대한 개념을 확실히 익힙니다.

Random Variable(확률변수)
Definition
1. 확률적인 결과에 따라 결과값이 바뀌는 변수를 묘사하는 통계학 및 확률론의 개념
2. 어떤 시행의 결과에 따라 변수 X가 가지는 값과, 확률이 정해질 때, 이 변수 X를 확률 변수라 함.
즉, 어떤 확률 공간에서 확률 값을 나타내는 특정 값이 될 수 있는 변수를 확률 변수라 합니다.
※ 확률 공간(probability space) : 전체 측도가 1인 측도 공간
※ 확률 변수는 대문자로 표기 ex : 확률변수 X
Example
자, 주사위를 던졌을 때,
주사위의 눈이 짝수가 나올 확률이 1/2
주사위의 눈이 홀수가 나올 확률이 1/2
이 되는 확률변수를 X라 하겠습니다.
이 때, 확률변수 X는 '짝수' 또는 '홀수' 가 될 수 있습니다.
Characteristic
Discrete Random Variable(이산확률변수) : 존재할 수 있는 값의 수가 유한한 경우, 확률 함수는P(X)
Continuous Random Variable(연속확률변수) : 존재할 수 있는 값의 수가 무한한 경우(어떤 범위에 속하는 모든 실숫값을 가질 때), 확률 함수는 P(a<= X <= b)
Probability Distribution(확률 분포)
Definition
확률 변수가 특정한 확률 값을 가지는 대응 관계
Characteristic
Discrete Probability Distribution(이산 확률 분포)
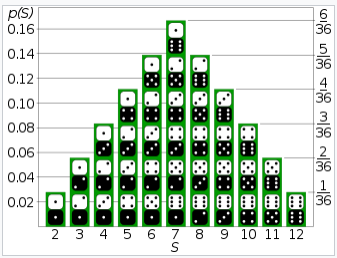
Continuous Probability Distribution(연속 확률 분포)

PDF(Probability Density Funciton 확률 밀도 함수)
Definition
연속 확률 변수의 분포(확률)를 나타내는 함수 \(f(x)\)
확률 밀도 함수 \(f(x)\) 와 구간[a, b]에 대해서 확률 변수 X가 구간에 포함될 확률
\(P(a\leq X \leq b) = \int_{a}^{b}f(x)dx\)
Example
Normal Distribution(m=0, σ=1)의 구간 1에서 2를 가질 확률 graph
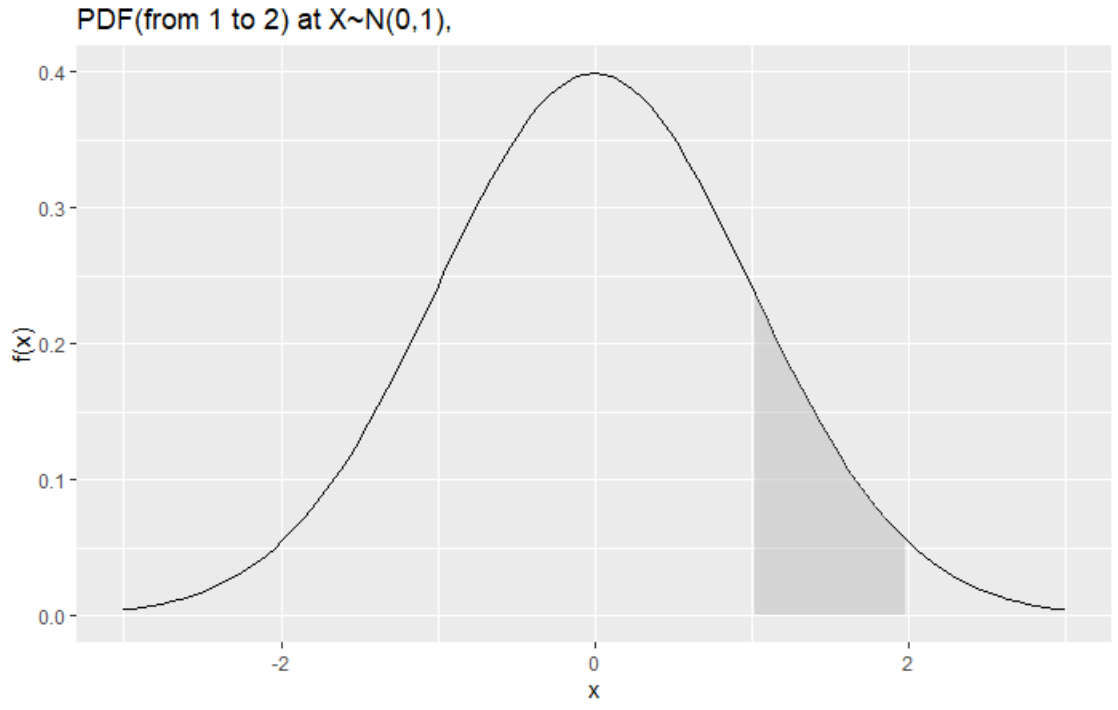
Characteristic
모든 실수값 x에 대해 \(f(x)\geq 0\)
\(\int_{-\infty}^{\infty}f(x)dx = 1\)
(CDF)\(F(x)=\int_{-\infty}^{x}f(x)dx\)
(PDF)\(f(x)=\frac{\mathrm{d} }{\mathrm{d} x}F(x)\)
CDF(Cumulative Distribution Function 누적 분포 함수)
Definition
연속형 분포의 주어진 확률 변수가 특정 값보다 작거나 같은 확률을 나타내는 함수
확률변수 X에 대한 확률을 \(P_{X}\) 라 하면 CDF는
\(F_{X}(x)= P_{X}(X \leq x)\)
Example
Normal Distribution(m=0, σ=1)의 모든 구간에 대한 CDF graph

Characteristic
\(F(-\infty) = 0\)
\(F(\infty) = 1\)
(CDF)\(F(x)=\int_{-\infty}^{x}f(x)dx\)
(PDF)\(f(x)=\frac{\mathrm{d} }{\mathrm{d} x}F(x)\)
PMF(Probability Mass Function 확률 질량 함수)
Definition
이산 확률 변수의 분포(확률)를 나타내는 함수
\(P(X=x_{i})=p_{i}\) (i=1,2,3, ... n)
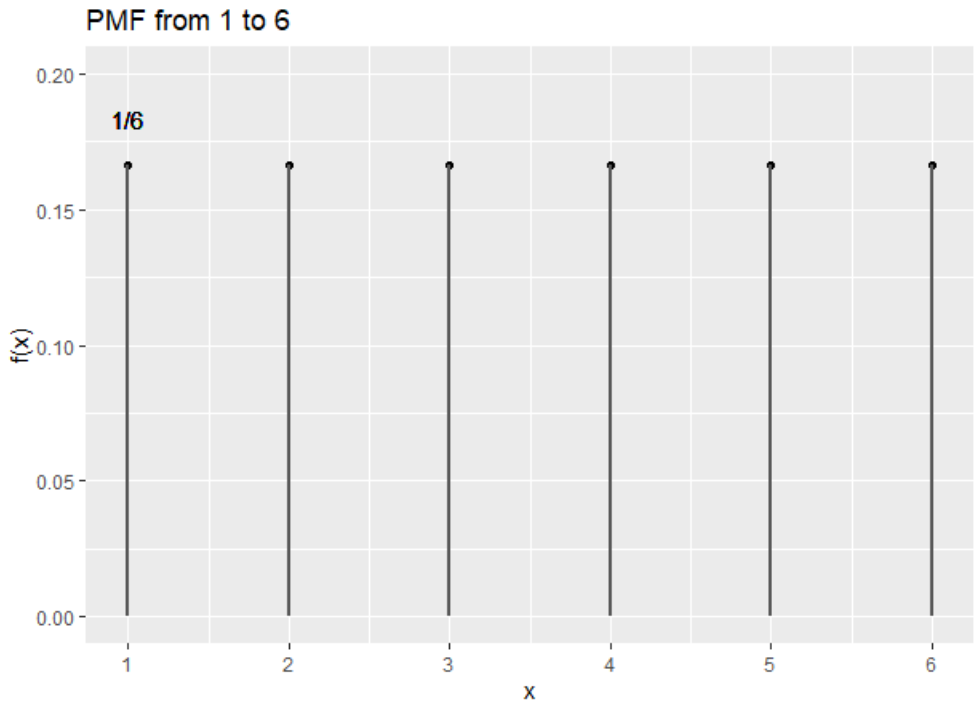
Characteristic
\(0\leq p_{i}\leq 1\)
\(\sum_{i=1}^{n}p_{i}=1\)
\(P(x_{i}\leq X \leq x_{j})=\sum_{k=i}^{j}p_{k}\)
CMF(Cumulative Mass Function 누적 질량 함수)
Definition
이산형 분포의 주어진 확률 변수가 특정 값보다 작거나 같은 확률을 나타내는 함수
큰 범위에서 CDF(Cumulative Distribution Function) 으로 그냥 부르기도 함.
\(F(x)=P(X\leq x)\)
\(F(x)= P(X \leq x) = \sum_{t \leq x}^{}f(t)\)

Characteristic
F(x) 를 CMF라하면 \(P(a< X \leq b) = F(b) - F(a)\)
'머신러닝 > 통계' 카테고리의 다른 글
| 통계 - T test (0) | 2021.03.26 |
|---|---|
| 통계 - Expectation E(X) (0) | 2021.03.24 |
| 통계 - Likelihood (0) | 2021.03.24 |
| 통계 - Statistical Estimation (0) | 2021.03.20 |
| 통계 - Normal distribution 어렵지 않아요 (0) | 2021.03.07 |